CHAPITRE 1 :

La loi des courants de Kirschoff - Le théorème de Thévenin - Le théorème de Norton - 

(Tous les énoncés des lois vues ici s'appliquent aux courants continus et alternatifs.)
La loi des courants de Kirschoff :


Aussi connue sous le nom de la loi des noeuds et des mailles , cette loi peut s'énoncer ainsi :

En appelant noeud une simple connexion entre plusieurs conducteurs on peut dire que :

la somme des courants convergeant vers un noeud est égale à la somme des courants qui en divergent


Cette loi d'apparence simple n'est pas toujours évidente à mettre en application.

Dans la littérature anglo-saxonne cette loi est appelée  KCL pour Kirschoff's Currents Law . (We apply KCL...)


Le théorème de Thévenin



Tout dispositif à sortie analogique ( par opposition aux dispositifs numériques ) peut être représenté complètement par deux éléments  :  un générateur de tension et sa résistance  (ou impédance) de sortie :

Cas du continu :


  on mesure toujours avec un voltmètre dont l'impédance d'entrée est équivalente à l'infini.

 En absence de charge sur la sortie la tension mesurée Vth dite tension de Thévenin est égale à B+ (puisque le courant est alors nul dans la résistance de sortie) .
La résistance de sortie Rs est appelée résistance de Thévenin.
Pour mesurer cette résistance on charge la sortie par une résistance RL égale à la résistance de Thévenin ( on procède avec une résistance variable ou un potentiomètre )  . On applique alors directement la loi d'ohm et la règle du diviseur de tension :

Si  RL = Rth  alors  Vs = B+ / 2
RL pour résistance de charge = Load en anglais
Cas de l'alternatif :


C'est la représentation qui diffère mais le raisonnement est le même. Eth est la tension de Thévenin en absence de courant dans Zth , impédance de Thévenin.


Avec une impédance de charge ZL  et si     

la tension Vs de sortie vaut :              
 



Ainsi n'importe quel étage amplificateur ou série d'étages d'amplification peut être complètement représenté ainsi :

Fig. 6
Nous avons ici une tension d'entrée Ve qui peut être un signal complexe. L'amplificateur a un gain de A. En absence de charge la tension  Vs = A x Ve. Sans aller plus loin pour le moment on voit que l'impédance de sortie Zs peut jouer un rôle très important.


Le théorème de Norton



Tout dispositif à sortie analogique ( par opposition aux dispositifs numériques ) peut être représenté complètement par deux éléments  :  un générateur de courant et une résistance (ou impédance)  en parallèle :

C'est le pendant au théorème de Thévenin mais en générateur de courant cette fois. Mais tout d'abord qu'est-ce qu'un générateur de courant ?

C'est un dipôle ( = deux pôles) représenté ainsi :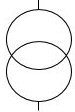


Le générateur de courant idéal représenté ici a pour caractéristique une impédance de sortie infinie, c'est-à-dire qu'il génère le courant pour lequel il est conçu quelle que soit l'impédance qu'on lui présente :




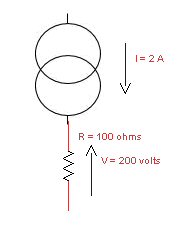On voit ici que si I = 2 A  et que R = 100 ohms la tension V aux bornes de R vaut 200 volts



Si   R  =  10  kOhms alors   V  =  20  000  volts !


Il va de soi qu'un tel générateur idéal n'existe pas dans la nature  !




En revanche il devient un composant tout à fait courant si on lui adjoint une impédance en parallèle :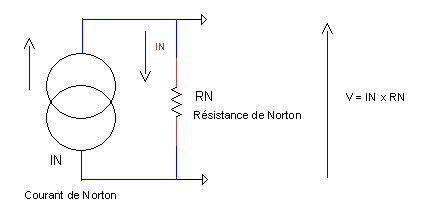


Ainsi tout comme avec le générateur de tension de Thévenin on peut réduire tout montage analogique à sa représentation en générateur de courant auquel on adjoint une résistance ou une impédance en parallèle.  Cette représentation est valable quel que soit  le régime du courant,  continu ou alternatif.

La tension qui apparaît en sortie d'un générateur de Norton suit naturellement la loi d'ohm, elle vaut :
V = IN x RN  

avec  IN = courant de Norton et RN = résistance ( ou impédance)  de Norton


Si l'on adjoint une impédance de charge en sortie du montage nous obtenons :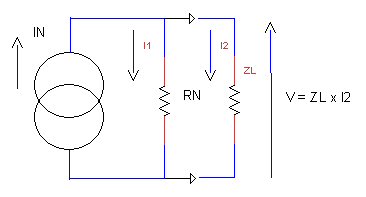


Depuis que nous avons vu le diviseur de courant nous pouvons écrire directement :


                                               RN                                             
I2 = IN  _______
          
                RN + ZL
D'où :
                 RN 
V = ZL IN  _______

                             RN + ZL          
               
                                          
Prenons maintenant un peu de recul :  nous avons dit que Thévenin et Norton étaient des représentations universelles auxquelles on pouvait réduire n'importe quel montage analogique . Si cela est vrai : pouvons nous vraiment choisir l'un ou l'autre indifféremment . En un mot sont-ils équivalents : absolument !


Reprenons la formule ci-dessus :
                 RN 
V = ZL IN  _______

                  RN + ZL

et arrangeons-là autrement :
                 ZL
V = RN IN  _______

                  RN + ZL


Nous voyons apparaître une tension Eth = RN IN  suivie d'un diviseur de tension ZL / (RN + ZL) dont le schéma serait :


avec  Eth   =  RN IN
Nous avons donc montré ici que le générateur de Norton caractérisé par son courant IN et sa résistance RN chargé par son impédance ZL était équivalent à un générateur de Thévenin  dont la tension serait :
Eth   =  RN IN

et la résistance de sortie :                           Rth = RN
C'est tout pour le moment pour ces deux théorèmes qui ouvrent bien des portes pour comprendre la théorie des amplificateurs.



Copyright ProjetG5 - Rédacteur jptrol
mis à jour le 24 mars 2007