Chapitre 3 : La triode (suite)
Montages en cathode commune ( amplificateur) :
Amplificateur triode en cathode commune partiellement découplée
Calcul de l'impédance d'entrée

(Schéma équivalent pour
l’alternatif)

Fig. 1

Fig. 1
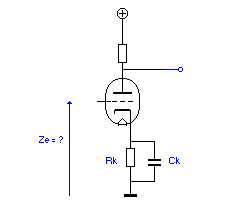
Le montage se présente comme le montage à
cathode découplée mais avec l'impédance Zk
représentant le réseau RK - CK à la cathode.
Ici encore le courant Ig étant considéré comme quasi nul, seul l'effet des capacités de la triode représentées ci-dessous va influer sur le signal d'entrée.
Sur la figure ci-dessous:
Cga est la capacité entre grille et anode.
Cgk est la capacité entre grille et cathode.
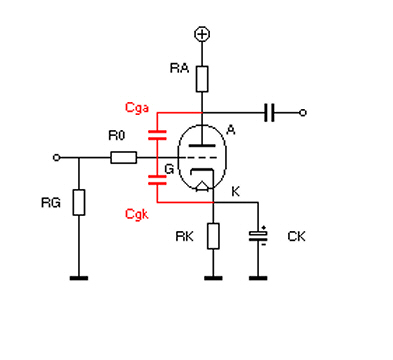
Fig. 2
Naturellement pour raisonner
il est nécessaire de retourner au schéma équivalent
pour l'alternatif :
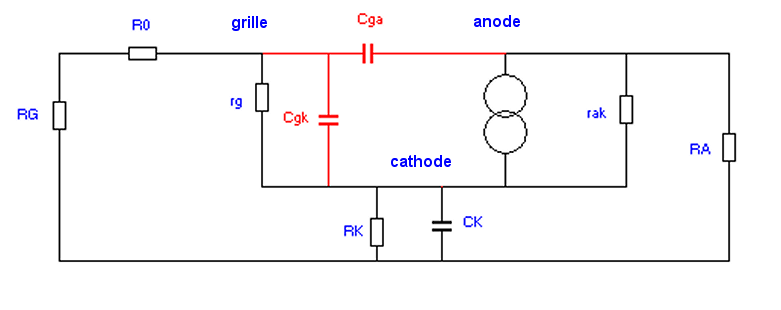
Fig. 3
Ici encore le courant Ig étant considéré comme quasi nul, seul l'effet des capacités de la triode représentées ci-dessous va influer sur le signal d'entrée.
Sur la figure ci-dessous:
Cga est la capacité entre grille et anode.
Cgk est la capacité entre grille et cathode.

Fig. 2

Fig. 3
Le théorème de
Miller appliqué ici donne de même la capacité
Cga multipliée par ( |A|+1) en entrée du montage avec
A = gain du montage en valeur absolue.
Bien que la cathode ne soit que partiellement découplée Cgk est encore de l'ordre du millionième de Ck, capacité de découplage, aussi peut on considérer que Cgk est à la masse à travers Ck.
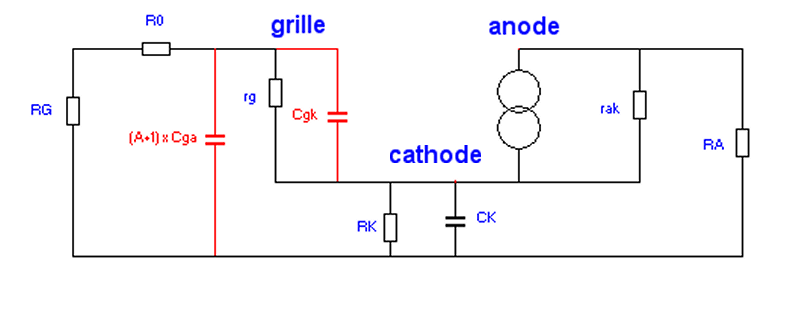
Fig. 4
Bien que la cathode ne soit que partiellement découplée Cgk est encore de l'ordre du millionième de Ck, capacité de découplage, aussi peut on considérer que Cgk est à la masse à travers Ck.

Fig. 4
Avec :
- rak = résistance interne de la triode ( cf Datasheet)
- rg = résistance de grille considérée comme très grande
- R0 = résistance de protection de la grille ( grid-stopper)
- RG =
résistance extérieure en entrée de l'étage
destinée à polariser la grille (voir
plus loin) dite résistance de fuite de grille ou
grid-leak resistor.
Le passe-bas en entrée est constitué de R0
et de la capacité équivalente à (|A|+1) x Cga
+ Cgk comme dans le cas du montage parfaitement
découplé. Nous savons que dans l'expression de A,
gain du montage, intervient l'impédance Zk :

En effet la cellule RC de
la cathode ne concerne que les fréquences basses
(ici on monte relativement haut car on a choisi
470 nF qui est une valeur limite, un cas d'école
pour ainsi dire). Sinon la fréquence de coupure à
-3 dB se situe souvent en dessous de 200 Hz et le
gain à 10 kHz est le même , que l'on soit
parfaitement ou partiellement découplé. En ce qui
concerne l'impédance d'entrée la conclusion
est donc la même que dans le cas de la cathode
parfaitement découplée.
L'échelle est en dB . Lorsque l'on s'approche du continu Zk tend vers Rk = 1500 ohms et rg est alors multipliée par 1,9 environ ( 5,6 dB). Lorsque l'on monte en fréquence , on tend vers 0 dB soit 1.
Rappelons que cette donnée n'a aucune valeur pratique, la valeur de rg n'étant pas même documentée dans les datasheets. Seules les capacités interelectrodes sont importantes.

La question devient : dans quelle
mesure l'impédance Zk intervient-elle dans la
valeur de la capacité (|A|+1) x
Cga + Cgk vue à l'entrée de l'étage ? La
réponse est simple, aux fréquences concernées,
c'est-à-dire au-dessus de 10 kHz, la cellule
Rk-Ck n'intervient pratiquement plus comme le
montre le graphe suivant donnant le gain en
fonction de la fréquence avec deux valeurs de
Ck, capacité de découplage :
En rouge : Ck = 22 µF la cathode est parfaitement découplée
En bleu : Ck = 470 nF la cathode est partiellement découplée.
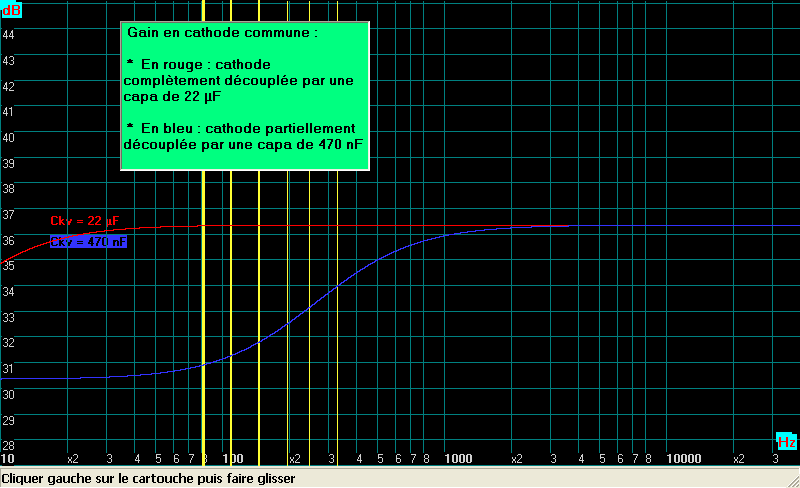
Fig. 5
En rouge : Ck = 22 µF la cathode est parfaitement découplée
En bleu : Ck = 470 nF la cathode est partiellement découplée.

Fig. 5
Note
:
D'un point de vue uniquement théorique et
sans aucun intérêt pratique ici,
on peut se poser la question de
l'influence de l'impédance Zk sur
l'impédance rg de grille du montage. On a
considéré
à raison
le courant ig traversant
rg comme négligeable. Si l'on en tenait
compte dans les calculs en reprenant la
Fig.1 on obtiendrait Ze = f( ig,rg,Zk) =
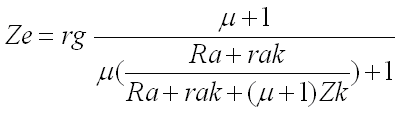
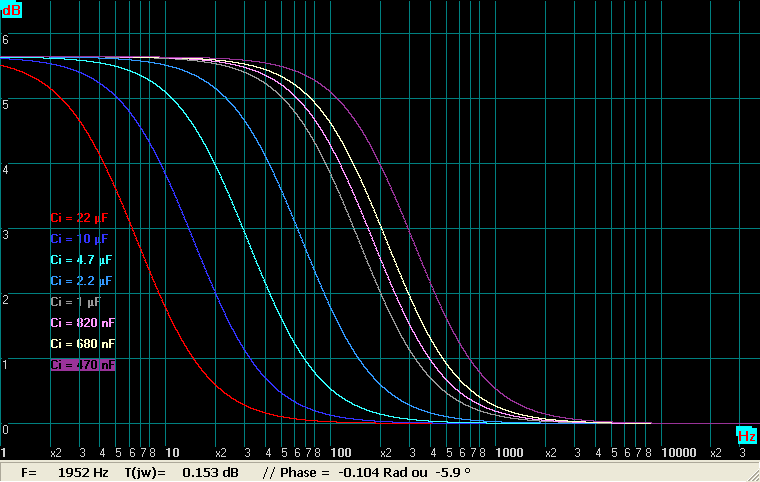
Pour différentes valeurs de capacités de découplage voici le facteur multiplicatif de rg en dB pour une valeur de Rk de 1500 ohms :
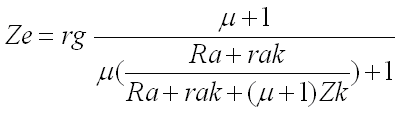
avec
Zk =


(la démonstration
est disponible uniquement sur demande
expresse !)
Cette
impédance est bien plus élevée que celle
calculée précédemment en faisant
intervenir en parallèle RG et R0 + ZCa. On
voit sur la formule que rg est multipliée
par un facteur dont la valeur minimum est
1 lorsque Zk vaut 0, c'est-à-dire lorsque
la cathode est parfaitement découplée !Pour différentes valeurs de capacités de découplage voici le facteur multiplicatif de rg en dB pour une valeur de Rk de 1500 ohms :

L'échelle est en dB . Lorsque l'on s'approche du continu Zk tend vers Rk = 1500 ohms et rg est alors multipliée par 1,9 environ ( 5,6 dB). Lorsque l'on monte en fréquence , on tend vers 0 dB soit 1.
Rappelons que cette donnée n'a aucune valeur pratique, la valeur de rg n'étant pas même documentée dans les datasheets. Seules les capacités interelectrodes sont importantes.