CHAPITRE 1 :

Qu'est-ce qu'une capacité  -  Qu'est-ce qu'une SELF ou INDUCTANCE ?






            Qu'est-ce qu'une capacité ?



C'est la capacité pour le composant électronique appelé condensateur de maintenir une charge électrique Q sous une tension U.
Expliquons-nous :  un condensateur est un dipôle formé de deux armatures se faisant vis-à-vis et isolées par un diélectrique . La technologie employée dépend de la nature du condensateur ( électrolytique ou chimique, en céramique, au mylar ,au polyester, au papier etc... on peut si on le veut voir quelques détails sur wikipedia sur les technologies employées).




Nous ne nous intéressons pas ici à la manière dont la charge s'est installée sur les armatures mais nous constatons que le courant continu ne peut passer, le diélectrique formant isolant.

La charge Q est exprimée en coulombs ( c'est une unité que nous pourrons oublier rapidement par la suite) .
Si l'on se place sur un conducteur et que l'on observe pendant 2 secondes passer un courant de 3 A , nous aurons vu passer 2 x 3 = 6 coulombs de charge  car :

    Q = I x t

Nous avons vu aussi que, par définition de la capacité :


    Q = C x U


C est la capacité exprimée en FARADS  c'est-à-dire le rapport constant entre la charge présente sur les armatures et la tension aux bornes de la capacité     C =  Q / U.

Un mot sur les unités utilisées :  un FARAD représente la capacité qui permet de maintenir un coulomb ( c'est-à-dire une charge équivalent à 1 A pendant une seconde) aux bornes d'un condensateur sous une tension de 1 volt.

Dans la réalité cette unité est beaucoup trop grande : on utilise :
  • le millionnième de FARAD  : le microfarad  µF    =  1e-6 F          (1e-6 = 1 dix puissance - 6)


  • le millième de milionnième de FARAD  :  le nanofarad  nF = 1e-9 F


  • le millionnième de millionnième de FARAD : le picofarad pF = 1e-12 F


Le plus souvent les capacités à partir de 1 µF sont électrochimiques et donc polarisées : elles possèdent un pôle + et un pôle - qu'il faut respecter dans les montages.

La deuxième caractéristique de la capacité est sa tension de claquage exprimée en volts bien sûr : il s'agit de la tension maximum au-delà de laquelle l'intégrité du diélectrique est compromise. Dans les montages on veille à rester bien en-dessous de cette tension limite : le choix de la capacité se fait avec une marge de sécurité conséquente.

Revenons maintenant à la charge :-) :

Il est évident que l'intérêt de la capacité ici est son comportement sous un régime de tensions et de courants variables puisque le continu ne passe pas.  Nous allons étudier le comportement de la capacité sous une tension alternative sinusoïdale puisque rappelons-le : tout signal , même le plus complexe, peut être décomposé en une multitude de simples signaux sinusoïdaux.


Pour le moment négligeons la résistance rg du générateur ci - dessus ( rg =~ 0)  pour nous intéresser au courant i qui circule dans la capacité.
Supposons donc que la tension aux bornes de C soit :
    (1)

 Pour qu'un courant circule dans C  il faut que la tension fasse varier constamment la charge aux bornes de la capacité . C'est le cas ici puisque la tension est sinusoïdale.
Puisque Q = CV  alors pendant un instant dt la charge va varier de dQ = C dV. Puisque Q = IT Le courant i résultant sera égal à dQ / dt d'où :


d'où l'on tire l'expression du courant :


Le courant i est donc égal à C multiplié par la dérivée de la tension V par rapport au temps t.
C'est ici qu'il faut faire appel à des souvenirs sinon à la conclusion de l'exposé sur les dérivées ici :
Y = sin (at)      =>  Y' = a sin (at + Pi/2)


donc  si  Y = V0 sin wt   alors  Y' = V0 w sin (wt + PI/2)   ( V0 étant ici une constante)
   
(2)

Si l'observe l'expression de la tension V0 sin (wt + PI/2) par rapport à celle présente aux  bornes de C, 
V0 sin (wt), on voit que c'est la même mais on a opéré une rotation de PI/2 sur la phase. C'est ici qu'il faut faire appel à des souvenirs sur les nombres complexes sinon à l'exposé  ici notamment sur les rotations 

En effet nous passons à partir de ce point dans un espace de calcul à deux dimensions qui ne nous quittera plus désormais dans nos raisonnements :  le fait d'ajouter PI/2 à la phase de la tension est équivalent à la multiplier par j. A partir de ce moment nous considérons V0 sin (wt + PI/2) et V0 sin (wt) comme des nombres complexes et l'on écrit :



d' où d'après (1) :



et d'après (2) :



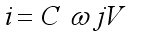en appliquant la loi d'ohm  ( V = Zc x I)



On tire alors la formule fondamentale donnant l'impédance de la capacité en fonction de la
fréquence  w = 2 Pi f de la tension appliquée à ses bornes :




On remarque au passage que le courant est en avance de 90° sur la tension puisqu'il faut multiplier celle-ci par j pour obtenir sa valeur. ( Cette remarque n'est pas fondamentale).





Mise en parallèle de capacités :

Intuitivement on voit que du fait que les surfaces des armatures s'additionnent la capacité sera la somme des capacités de chaque condensateur :


On applique la formule des résistances en parallèle (valable aussi pour les impédances !) :





Mise en série de capacités ( d'usage for limité) :

On devine moins intuitivement le résultat : les impédances s'ajoutent (comme les résistances).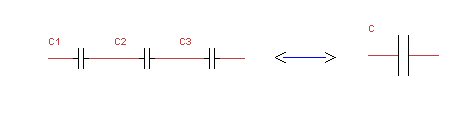



On utilise ce montage lorsqu'il s'agit de diviser les tensions de claquage  (très rare).





              Qu'est-ce qu'une SELF ou INDUCTANCE ?


On aborde ici l'électromagnétisme qui est un peu plus compliqué. Il s'agit d'exposer quelques notions pour comprendre les transformateurs et les selfs utilisées dans le filtrage des alimentations ainsi que le principe des micros de guitare.
Accessoirement cela permet aussi de comprendre les problèmes de parasitage ( hum).
Les explications sont simplifiées au maximum. Tout comme nous avons démontré pour les capacités que l'impédance était fonction de la fréquence  Zc = 1 /  jCw , nous allons voir qu'il en va de même pour les selfs où nous allons démontrer que l'impédance d'une self d'inductance L vaut ZL = jLw.

Mais d'abord qu'est-ce qu'une inductance ? 

Tout courant I parcourant un conducteur génère un champ magnétique H  comme ceci :


Fig.7
Le champ magnétique H tel qu'il apparaît ici s'exprime en ampères par mètre. On voit qu'il est à la fois directement proportionnel au courant et inversement proportionnel à la distance au conducteur. Plus on s'éloigne du conducteur, plus le champ faiblit.

L'induction magnétique B est directement proportionnelle au champ magnétique H . Le rapport entre l'induction et le champ dépend du milieu dans lequel ce champ se propage : l'air ( pour une self à air) ou un entrefer ( self à noyau ou transformateur ) .  Le rapport µ s'appelle la perméabilité magnétique du matériau :
B = µ H


L'induction magnétique B s'exprime en Teslas . Pour le vide ou l'air c'est la constante µ0 qui est utilisée : B = µ0 H . Pour un noyau de ferrite on multiplie cette valeur µ0 par la perméabilité propre au matériau. Ainsi on peut remplacer sur la figure 7 ci-dessus le vecteur H par un vecteur B représentant l'induction magnétique générée par le courant I.


Si l'on referme le conducteur de la figure 7  sur lui-même on obtient une spire de surface S emprisonnant une induction magnétique moyenne : cf. fig 8 ci-dessous :

Fig.8



La force électromagnétique que l'on va récupérer de ce dispositif va bien sûr dépendre à la fois de l'induction B ( donc du courant I ) et de la surface S sur laquelle s'exerce cette induction. C'est  la notion de  flux magnétique qui renferme celle de force électromagnétique.
Le flux magnétique est égal  au produit  B par S


Le rapport entre le flux magnétique et le courant I  qui parcourt la spire est constant :  c'est l'inductance   L    exprimée en Henrys





Si l'on empile N spires  , le champ H donc l'induction donc le flux sera multiplié par N :



Considérons maintenant la self suivante simplement constituée de N spires et traversée par un courant I. Sa longueur est l :

L'application directe du théorème d'Ampère pour une self à air donne :



On démontre à partir de cette relation que l'inductance L est entièrement dépendante des caractéristiques physiques de la self :
  •  longueur,
  •  nombre de spires 
  •  surface de la spire
  •  perméabilité magnétique du milieu
En effet :








d'où :



si le noyau de la self est un corps doué de propriétés magnétiques et de perméabilité µ alors


Rappelons que L en henrys est le rapport constant entre la variation du flux et la variation du courant :

-  si l'on fait varier I le flux varie proportionnellement à L  : ex la self , le primaire du transformateur, la bobine du haut-parleur
-  si l'on fait varier le flux , I  varie proportionnellement à L : ex : le micro guitare, le secondaire du transformateur.



Force électromotrice d'auto-induction :

La particularité de la self est de générer à ses bornes une tension e qui s'oppose aux variations du courant et donc du flux magnétique . Elle est appelée  force électromotrice d'auto-induction .Lorsque le flux (ou le courant) ne varie pas cette tension est nulle. Si le flux augmente , la tension croît avec le signe opposé . On écrit donc cette tension en fonction de l'accroissement dpendant l'instant dt :
(3)
Comme nous savons déjà que :



nous pouvons écrire en considérant qu'une variation de flux dest proportionnelle à une variation de courant di que  :



Si l'on reporte dans (3) cela donne :



La force électromotrice d'auto-induction est donc proportionnelle à la dérivée du courant traversant la self.

En considérant ce courant sinusoïdal de la forme :


la dérivée de ce courant s'écrit (revoir au besoin le rappel sur la dérivée ici) :


et donc :


Ici il faut faire appel à nouveau à des souvenirs sur les nombres complexes sinon à l'exposé  ici notamment sur les rotations .

Le fait d'ajouter PI/2 à la phase du courant est équivalent à le multiplier par j. A partir de ce moment nous considérons I0 sin (wt + PI/2) et I0 sin (wt) comme des nombres complexes et l'on écrit :



Nous en tirons :



Si nous retournons aux principes de la loi d'ohm :



Nous voyons à droite la représentation de la tension d'auto-induction de signe contraire au courant qui traverse la self.  Du point de vue de la loi d'ohm cette tension e = - U = - ZI.

D'où nous déduisons :



L'impédance Z d'une self pure vaut donc :



Si l'on se souvient que  w ( en radians/seconde ) = 2 Pi F  (Hertz) on voit que cette impédance est proportionnelle à la fréquence de la tension aux bornes de la self :  une self oppose une impédance d'autant plus forte au courant que la fréquence du signal est élevée. 
A contrario un courant continu ( w = 0) rencontre une impédance nulle.

Dans la réalité on représente en plus la résistance ohmique du fil de cuivre r :
L'impédance Z est un nombre complexe cette fois avec une partie réelle et la valeur ohmique de l'impédance est le module du nombre Z :



Dans la représentation schématique r est en série avec  jLw :


Représentation complète d'une self.


Copyright ProjetG5 - Rédacteur jptrol
mis à jour le 8 mai 2007