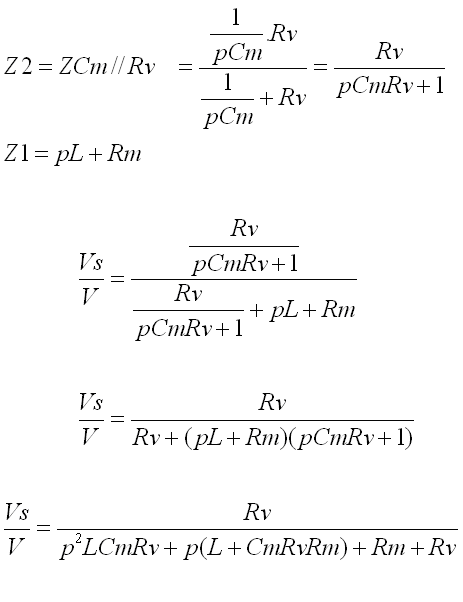INTRODUCTION :
Rappelons d'abord que la fonction de transfert ou transmittance est entendue ici comme le rapport entre la tension de sortie d'un montage et la tension d'entrée en fonction de la fréquence du signal. Revoir au besoin ici ces notions ainsi que l'expression de ce rapport en décibels.
Il ne faut pas perdre de vue que tous les calculs sans exception se font dans un espace à deux dimensions, c'est-à-dire pratiquement dans le plan <<complexe>> et ceci pour tenir compte du déphasage des signaux induit par les diverses capacités et inductances. Toute autre approche est vouée à l'échec.
On peut faire la démonstration en adoptant le raisonnement du <<débutant>> , sans notation péjorative, bien sûr, ce texte lui étant en particulier destiné.
Exemple à ne pas suivre : soit le réseau RC parallèle suivant.

Je veux
calculer l'impédance de ce réseau à la fréquence de
50 Hz et je ne m'intéresse pas au déphasage (grave
erreur !) . Je calcule donc l'impédance Zc de la
capacité C à la fréquence de 50 Hz soit :


Ensuite
cette impédance Zc étant en parallèle avec la
résistance R je calcule l'impédance globale avec
R en parallèle de Zc comme si Zc était une
résistance. Je trouve 100 k // 96457 = 49098
ohms. ( = R x Zc / ( R + Zc) ).
La réalité est bien différente : Zc est une impédance complexe que nous noterons dorénavant 1 / pC avec p = jw. p va devenir la variable nous permettant dorénavant <<d'oublier le côté complexe>> des calculs lorsque nous utiliserons l'ordinateur.
Pour le moment le calcul (manuel !) complet donne :


La réalité est bien différente : Zc est une impédance complexe que nous noterons dorénavant 1 / pC avec p = jw. p va devenir la variable nous permettant dorénavant <<d'oublier le côté complexe>> des calculs lorsque nous utiliserons l'ordinateur.
Pour le moment le calcul (manuel !) complet donne :


On
trouve donc au lieu de nos 49 kohms , en
réalité 69 kohms soit une erreur de 41,4
% ! ( racine de 2 en fait). On imagine que même
pour un résultat approché ce mode de
raisonnement ne peut être valable.
LA BONNE METHODE :

LA BONNE METHODE :

Sur
le schéma ci-dessus A , gain ou
atténuation suivant la nature du circuit
est en fait la transmittance ou la
fonction de transfert dès lors qu'il
sera fonction de la fréquence du signal
Ve entrant.
On peut réduire
tout circuit en quotient de deux
polynômes
fonction de la fréquence f du signal entrant en Herz (voir note).
fonction de la fréquence f du signal entrant en Herz (voir note).
La variable f
est transformée en radians /
seconde par la formule :

Puis on tient compte de la
phase du signal en effectuant les
calculs dans le plan à deux
dimensions : le plan complexe. La
variable devient jw avec j
opérateur imaginaire . Pour
simplifier la notation on adopte
celle des automaticiens qui
remplacent jw par p :

Ainsi il
suffit de noter les impédances
des capacités
et celles des inductances pL
pour que les polynômes s'organisent autour de
la variable p et que la tâche
revienne à l'ordinateur de s'en occuper !
Le polynôme générique est de la forme :

et la phase pour la fréquence f =

Exemple simple n° 2 :
L'étage d'entrée Hi du Marshall JCM800 monté en cathode partiellement découplée. On le prend ici chargé uniquement par RA ( cas d'école).


Le polynôme générique est de la forme :
On organise le numérateur
et le dénominateur en puissances décroissantes
de p, la variable. Tous les autres termes N[]
et D[] sont des constantes qui combinent les
valeurs des composants du circuit. Une
fois que l'on a cette équation sur le papier
on a fini ! On laisse à l'ordinateur la
mission pour nous harassante voire
abrutissante de mener les innombrables calculs
itératifs.
L'ordinateur est programmé comme ceci :
L'objectif est de séparer les parties réelles et les parties imaginaires afin de réduire le quotient à :

L'ordinateur est programmé comme ceci :
L'objectif est de séparer les parties réelles et les parties imaginaires afin de réduire le quotient à :

Si on se souvient que
:


on en déduit
que toutes les puissances paires de
p donnent des nombres réels et sont
à ajouter à X pour le numérateur et
W pour le dénominateur. De même les
puissances impaires de p donnant des
nombres imaginaires sont à ajouter
respectivement à Y et Z.
Un fois le calcul effectué pour la fréquence f ( p = j 2 pi f) on trouve la magnitude de A ainsi
Un fois le calcul effectué pour la fréquence f ( p = j 2 pi f) on trouve la magnitude de A ainsi

et la phase pour la fréquence f =
Note : En théorie
c'est vrai mais dès que les circuits se
compliquent il est beaucoup plus rationnel
de faire appel à d'autres outils
mathématiques, en l'occurrence le calcul
matriciel qui permet de résoudre les
systèmes de n équations à n inconnues
. C'est ainsi que procède SPICE. Ceci sort
de l'objet de cet article.
On l'aura compris, la
vraie difficulté réside dans l'établissement
de l'équation.Le principe est cependant
toujours le même : une fois qu'on a une
construction à plusieurs étages il suffit de
multiplier haut et bas par les dénominateurs
les plus bas . On répéte l'opération jusqu'à
obtenir une expression en puissances de p
comportant un numérateur et un dénominateur.
Si vraiment la construction est complexe on peut toujours demander à l'ordinateur de multiplier des polynômes entre eux. L'exemple de logiciel disponible ici sait multiplier trois polynômes entre eux.
Si vraiment la construction est complexe on peut toujours demander à l'ordinateur de multiplier des polynômes entre eux. L'exemple de logiciel disponible ici sait multiplier trois polynômes entre eux.
| Exemple simple n° 1 : | Montage
passe-haut |
| Exemple simple n° 2 : | Entrée
JCM800 triode en cathode commune
partiellement découplée |
| Exemple n° 3 : | Polynôme du
second degré: micro
guitare amorti sur pot
de volume seul |

Ici les numérateur et
dénominateur sont du premier degré et dans le
polynôme générique ci-dessus on peut
identifier facilement N[1] = RC , N [0] = 0 ,
D[1] = RC et D[0] = 1.
Exemple simple n° 2 :
L'étage d'entrée Hi du Marshall JCM800 monté en cathode partiellement découplée. On le prend ici chargé uniquement par RA ( cas d'école).


Zk est l'impédance de Rk
en parallèle sur Ck dont nous avons calculé la
formule justement en haut de cette page.





reportée dans
l'expression du gain :

développée en
multipliant haut et bas par le plus bas
dénominateur :

organisée en polynôme
( du premier degré ici ) et en respectant
le signe - pour tracer correctement le
graphe de la phase :

Par rapport au polynôme générique on
voit apparaître les constantes à entrer dans
l'ordinateur :
On prend pour exemple un micro guitare modélisé le plus simplement en 3 composants :
N[1] = - RkCkµRAExemple n° 3 : Polynôme du second degré .
N[0] = - µRA
D[1] = RkCk(RA+rak)
D[0] = RA + rak + (µ+1) Rk
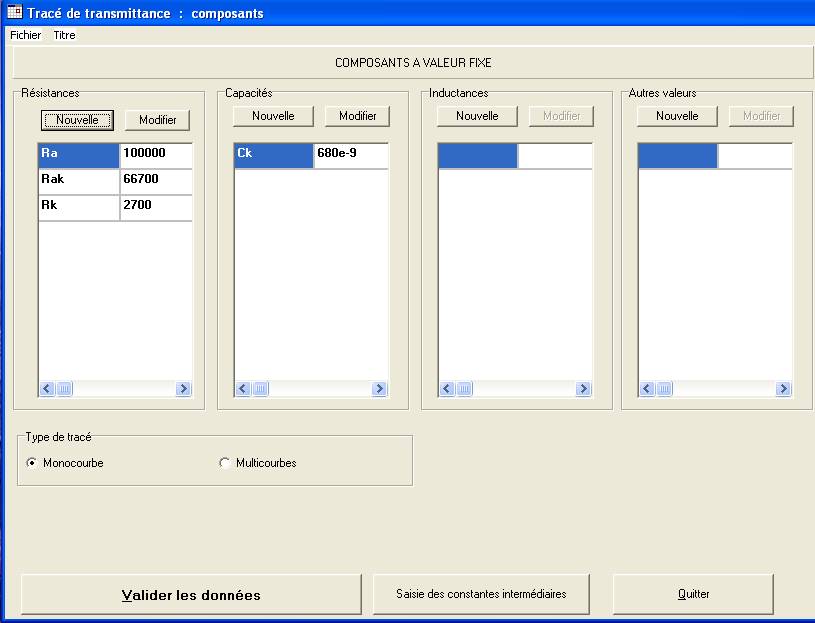
Donc après avoir entré les valeurs des composants :
puis les 4 constantes ci-dessus
il suffit de valider et lancer le tracé qui donne :
Sur le graphe des magnitudes on voit apparaître le palier supérieur lorsque p tend vers l'infini et le palier inférieur lorsque p tend vers 0.
Quand p tend vers l'infini :

C'est la formule du gain avec la cathode parfaitement découplée ( Ck est alors un court-circuit)
Quand p tend vers zéro :
C'est la formule du gain avec la cathode non découplée ( Ck est alors un circuit ouvert)
On voit que c'est la grandeur (µ+1) Rk qui détermine l'écart entre le palier bas et le palier haut (en rapport avec RA+rak tout de même) que Merlin Blencowe et Randall Aiken appellent le << GAP>> et sur lequel jouent les concepteurs d'ampli pour personnaliser la tonalité. Cet écart est pour l'entrée HI du JCM800 de 35,5 - 27,1 = 8,4 dB. Sur la charge réelle le palier haut atteint 35 dB et le palier bas est beaucoup plus bas et progressif grâce aux filtres qui suivent pour attaquer l'étage 2.
On prend pour exemple un micro guitare modélisé le plus simplement en 3 composants :
une self Lm
une résistance Rm ( en série avec la self)
une capacité Cm à la masse
Cette impédance est chargée par une simple résistance fixe Rv matérialisant le potentiomètre de volume.
Le schéma est le suivant :
Le rapport Vs / V est un simple diviseur de tension :
On applique toujours le même principe consistant à multiplier haut et bas par le plus bas dénominateur. On obtient ici une constante Rv divisée par un polynôme du second degré en p.
Par rapport au quotient générique de polynômes on identifie alors les constantes :
N[0] = Rv pour le numérateur
et pour le dénominateur :
D[2] = L*Cm*Rv
D[1] = L+Cm*Rv*Rm
D[0] = Rm + Rv
On entre alors les composants en premier lieu :
Puis on valide les données et l'on entre alors les constantes en prenant l'option polynôme :
Après validation on lance simplement le tracé :