CHAPITRE 1 :
Comme
nous le disions à l'article
"bande
passante", dans le
domaine de l'audio les
fréquences audibles
s'étalent d'environ 16 Hz
à 20 000 Hz.
Tous les dispositifs qui ne transmettent pas intégralement toutes les fréquences présentes en entrée filtrent celles-ci. On peut par exemple choisir de transmettre les fréquences basses et atténuer les fréquences aigües. On a alors affaire à un filtre passe-bas. Si l'on choisit au contraire de retenir les fréquences aigües et d'atténuer les fréquences basses on a affaire à un filtre passe-haut. Nos amplis guitare renferment un certain nombre de filtres plus ou moins complexes. Le plus complexe est le tone-stack (l'ensemble correcteur de tonalité) constitué de résistances dont certaines variables ( les potentiomètres) et de capacités . Nous verrons plus loin que les étages d'entrée de chaque module amplificateur constituent des passe-bas. Nous verrons aussi que chaque dispositif de couplage entre les étages constitue un passe-haut. Ces deux derniers ne répondent pas à un effet recherché mais plutôt à une contrainte technologique qu'il est impératif de prendre en compte. La compréhension des simples filtres passe-bas et passe-haut permet de bien calculer les bandes passantes et de maîtriser les outils de détermination modernes ( logiciels) des tone-stacks. FILTRE
PASSE-BAS
:
Un
filtre passe-bas
élémentaire est constitué
d'une résistance et d'une
capacité :
 Nous
savons déjà ( revoir qu'est-ce
qu'une
capacité ) que
l'impédance de la capacité
décroit lorsque la fréquence
croît ( Zc = 1 / j
Cw avec w = 2 Pi f)
. Nous voyons donc que
pour une fréquence infinie
nous aurons un court-circuit
franc sur la capacité et que
Vs = 0. A contrario lorsque w
= 0, c'est-à-dire pour une
fréquence nulle (c'est ainsi
que l'on peut aussi
parler
du courant continu :
c'est un courant
alternatif de fréquence
nulle) donc si w =0 ,
alors Zc est infinie et
Vs = Ve. Un passe-bas laisse
donc passer le courant
continu.
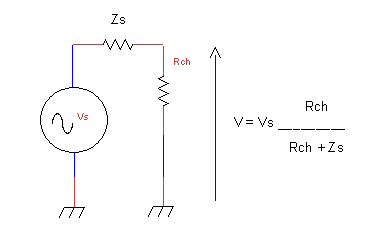
Considérons
le schéma ci-dessus constitué
de deux impédances Z1 et Z2 :
 Nous
savons que Z1 = R
et Z2 = 1 / jCw.
Nous pouvons donc écrire que
la transmittance
T(jw) = Vs / Ve vaut:
 L'expression
complexe du passe-bas est donc
:
 Nous
retrouvons ce que nous disions
plus haut : si w = 0
alors Vs = Ve . Si w = infini
alors Vs = 1 / infini = 0.
Notre raisonnement sur les filtres est à rapprocher de celui sur la bande passante . L'intérêt est maintenant de connaître la fréquence de coupure fc c'est-à-dire la fréquence à partir de laquelle la puissance en sortie chute de moitié. Ici nous dirons que c'est la fréquence pour laquelle le rapport des tensions est de 1 / racine de 2 = 0.707 ( revoir l'exposé au besoin ). Ainsi la bande passante de notre filtre sera de 0 Hz à fc Hz Le module de notre nombre complexe est ici :  La
fréquence de coupure
correspondra à :
 d'où
il vient :
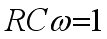   Comme
nous l'avons vu à
l'article sur les dB
cette fréquence est celle où l'atténuation
du
filtre est de - 3 dB.
Ainsi
toutes les fréquences
supérieures à fc sont
considérées comme atténuées .
Nous allons voir comment se présente la courbe de réponse d'un filtre passe-bas : - en abscisse nous lisons les fréquences sur une échelle logarithmique qui permet de voir sur une plage plus large. - en ordonnée nous lisons les rapports Vs/Ve en décibels .  L'échelle
des fréquences s'étale ici
de 1 Hz à environ 8 kHz.
La fréquence de coupure à
-3 dB est à peu près à 33,8
Hz. Avec les valeurs de R =
470 ohms et de C = 10 µF la
fréquence de coupure exacte
est de f = 1 / 2 Pi RC =
33,8628 Hz.Accessoirement on peut aussi tracer la réponse en phase, bien que ce ne soit pas très utile pour nos problèmes d'ampli guitare :  On voit ici en ordonnée l'angle de déphasage en fonction de la fréquence . Celui-ci va de 0° à - 90° ( ou - Pi/2) lorsque la fréquence tend vers l'infini. A la fréquence de coupure fc le déphasage est de - 45° ou - Pi/4. Afin de simplifier les calculs de bande passante d'un étage amplificateur à triode que nous verrons plus loin , il est nécessaire de bien comprendre pourquoi notre fréquence de coupure est déphasée de - 45 ° Revenons à l'expression de la transmittance :  A la fréquence de coupure : RCw = 1 donc cette transmittance vaut 1 / 1 + j. Le déphasage est donc l'argument de ce nombre c'est - dire : arg (1) - arg (1+j) = 0° - 45° = - 45°. (revoir les nombres complexes si nécessaire). ________________________
Filtre passe-haut : Un filtre passe-haut élémentaire est aussi constitué d'une résistance et d'une capacité :  Nous voyons ici que le continu ( fréquence = 0 - cf plus haut) n'est pas transmis . La capacité présente une impédance décroissante à mesure que la fréquence croît. Ainsi Vs = Ve lorsque cette fréquence est inifinie : nous avons bien un passe haut. Si l'on reprend le principe du diviseur de tension vu avec le passe-bas ci-dessus avec Zc = impédance de C = 1 / jCw nous avons :  Nous retrouvons ici le raisonnement sur le schéma : Si w tend vers l'infini Vs/Ve tend vers 1 ( 0 dB) . Si w = 0 alors Vs/Ve = 0 et Vs = 0 donc l'atténuation est maximale et nous avons bien un passe-haut. Nous allons donc calculer la fréquence de coupure fc à partir de laquelle la transmittance dépasse - 3dB et tend ensuite vers 0 dB En appliquant toujours le même principe , puisque dans la bande passante le rapport est de 1 ( 0 dB) à la fréquence de coupure le rapport sera de 0.707 ( 1 / racine de 2). ( revoir la notion de bande passante au besoin). Donc à fc :  D'après
ci-dessus le module de la
transmittance vaut :
 et :
 d'où il
vient :
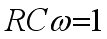 tout comme sur le passe-bas !   Il n'y a donc qu'une seule formule à retenir pour les deux types de filtres. La courbe de réponse du passe-haut tracée suivant les principes vus ci-dessus se présente donc ainsi ( exemple pour R = 470 kOhms et C = 22 nF) :  La
fréquence de coupure à - 3
dB est de 1 / 2 Pi 470000
22e-9 = 15,39 Hz.
La courbe de réponse en phase est ici la suivante :  Le tracé est fait ici entre 0,1 Hz et 8 kHz. On voit que pour les fréquences proches du 0 le déphasage est de + 90° ou + Pi/2. Pour les fréquences dans la bande passante le déphasage tend vers 0°. Ici le déphasage à la fréquence de coupure est de + 45° . En effet :  Avec RCw = 1 nous avons Vs/Ve = j / 1 + j. Le déphasage est donc arg (j) - arg (1 + j) = 90° - 45° = 45°. Ceci termine l'exposé sur les filtres élémentaires dont le calcul est fondamental pour réaliser nos amplis guitare.
Maintenant que les bases sont installées, posons nous la question de la conception des étages de notre ampli : si nous concevons un étage , nous devons nous poser les questions suivantes :
Ces
3 aspects caractérisent tout
quadripôle
au sens où nous l'avons vu
plus haut.
LA POLARISATION : Prenons un schéma très simple comme le suivant ( c'est un cas d'école ici ). 
La tension B+
est la tension
d'alimentation
continue. Les
tensions
continues sont
fixées par la
valeur des
résistances et
donc le courant
continu Ip dit
de
polarisation .
Nous
avons deux
valeurs de
tension aux
bornes de R2 :
En ce qui concerne les montages amplificateurs à triode ou pentode le problème de la polarisation est capital et fera l'objet d'un chapitre complet. Il répond aux mêmes impératifs que ci-dessus : fixer les potentiels des tensions continues au repos. LE
COMPORTEMENT EN
ALTERNATIF :
PRINCIPE
DU SCHEMA DIT
EQUIVALENT POUR
L'ALTERNATIF
Lorsque
l'on étudie la
propagation du
signal
alternatif (
celui qui nous
intéresse en
fait dans la
production du
son )
on
simplifie le
problème en
faisant
abstraction de
tous les
éléments liés
au courant
continu. On
établit le
schéma
équivalent
pour
l'alternatif,
dit aussi pour
petits signaux
car leur
amplitude en
tension est
bien sûr plus
faible que les
tensions
d'alimentation.
En
effet dans tous
les montages
nous avons en
sortie
d'alimentation
au moins une
grosse capacité
électrolytique
de filtrage de
la résiduelle du
secteur (
l'étude des
alimentations
fera l'objet
aussi d'un
chapitre
séparé).
Ci-dessous nous
donnons
l'exemple d'une
capacité de 470
µF. Pour
l'alternatif
nous pouvons la
remplacer par un
court-circuit,
son impédance
étant nulle aux
fréquences
audio. Le noeud du problème est de considérer que la tension d'alimentation B+ est en court-circuit pour l'alternatif.  A partir de ce moment le schéma se présente ainsi : 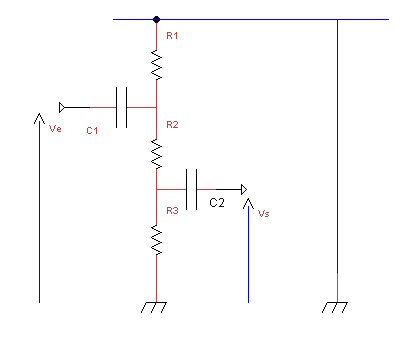 En
repérant
bien la tension
d'entrée Ve et la
tension de sortie Vs
, nous voyons bien
maintenant que R1 est à la
masse et le
schéma se simplifie
comme suit :
 Pour
simplifier encore
dans un premier
temps , nous pouvons
considérer que les
capacités C1 et C2
sont choisies pour
avoir une impédance
très faible par
rapport aux
résistances. On les
assimile alors à des
court-circuits pour
l'alternatif et le
schéma se présente
alors ainsi :
 A
chaque fois que l'on
parle ici de mesure
ou de calcul on
parle de la même
chose : on fait la
même chose avec une
calculatrice devant
un schéma qu'avec un
générateur BF et un
multimètre devant un
montage :
 Soit
I le courant
d'entrée :
l'impédance d'entrée
Ze vaut :
 Pour la mesure ici il est simple de mesurer I2 qui vaut Vs / R3 et I1 qui vaut Ve / R1 , de faire la somme I = I1+I2 puis de calculer Ze = Ve / I.  La
mesure standard de
l'impédance d'entrée
pour les montages
plus complexes
s'effectue avec un
voltmètre et un
ampèremètre :
 Mais
sans faire aucune mesure on
peut dire que nous allons
trouver ici une impédance
d'entrée qui vaut
 (revoir au besoin la mise
en parallèle de
résistances)
(revoir au besoin la mise
en parallèle de
résistances)En développant on écrit :  Mais il est plus simple de garder la notation : Ze = R1//(R2+R3) A partir du
moment où nous connaissons
l'impédance d'entrée Ze nous
pouvons reconsidérer la
capacité de couplage C1 et
vérifier la bande passante
du filtre
passe-haut ainsi formé
:
 Principe
du
calcul et de la mesure de
l'impédance de sortie :
Le principe
est le suivant :
 L'impédance
de sortie est :
 Par le calcul il vient de l'analyse simple du schéma :  Retenir
de ce calcul que pour mesurer
ou calculer l'impédance de
sortie d'un montage on court-circuite
l'entrée et on mesure
l'impédance vue sur la
sortie en branchant
un générateur.
Attention néanmoins : lorsque l'on dit que l'on court-circuite l'entrée pour mesurer l'impédance de sortie, il faut considérer si cela correspond au circuit en situation avec son étage précédent. Si l'impédance de sortie de l'étage précédent est non négligeable et que nous sommes en présence d'un circuit passif, celle-ci doit être prise en compte. Nous devons faire le schéma suivant : 
Nous pouvons considérer alors le résultat :  L'impédance
de
sortie
est toujours :
 Mais elle vaut
maintenant :
 En pratique on utilise, en mesure uniquement et pour éviter ce genre d'ambiguité, une autre méthode :
Fonction
de transfert ou transmittance
du montage :
Si nous reprenons le schéma fonctionnel équivalent sur notre circuit à trois résistances nous voyons tout de suite le rapport entre Vs et Ve : c'est un simple diviseur de tension avec R2 et R3 :   Il
s'agit donc d'un simple
atténuateur.
En adoptant le schéma universel de tout quadripôle amplificateur ou atténuateur nous pouvons dire que le schéma de gauche ci-dessous est équivalent au schéma de droite pour l'alternatif :
Si l'on prend en compte la remarque sur l'impédance de sortie Zs1 de l'étage précédent alors le schéma équivalent devient :   Nous verrons plus loin qu'un étage à circuit actif ( amplificateur ou directement adaptateur d'impédance) permet de mieux isoler les impédances d'entrée et de sortie). On peut ici donner le schéma universel auquel on peut rapporter tout montage :  Sur
ce schéma sont représentés :
En charge nous
aurons : Vs = A.Ve. ZL /
(ZL + Zs)
Pour
que le montage soit un amplificateur
il suffit que la valeur
absolue de A soit
supérieure à 1. On
parle en effet de valeur
absolue car le signe de A
détermine la phase du signal
par rapport à l'entrée. Si
Vs est en opposition de
phase avec Ve alors A est
négatif.
Si la valeur absolue de A est inférieure à 1 , le montage est atténuateur. Générateur de tension / générateur de courant : Nous avons donné ci-dessus un schéma universel sur le modèle du générateur de tension ( ou, avec son impédance de sortie, générateur de Thévenin ). Nous pourrions donner le même schéma en prenant pour modèle un générateur de courant ( ou , avec son impédance de sortie, générateur de Norton ).
Les deux schémas sont équivalents. Mais alors quelles sont les caractéristiques du générateur de Norton ? Nous nous rappelons que Eth = IN RN et que Rth = RN (revoir au besoin la conclusion sur le théorème de Norton ). Nous en déduisons que Z ( à droite ) = Zs ( à gauche ) : c'est l'impédance de sortie RN ou Rth. Le courant I du générateur vaut IN = Eth / RN = A Ve / Zs Le modèle universel en courant se présente donc ainsi :  Le courant I généré par le générateur vaut I = A.Ve / Zs Nous pouvons
faire une rapide
vérification en
appliquant le
diviseur de courant sur
les
impédances Zs et ZL. Le
courant I'
dans ZL vaut
I' = I . Zs / (Zs
+ ZL). Donc Vs
= I'. ZL = I
. ZLZs / (Zs + ZL)
D'où Vs = A.Ve .ZL / (Zs + ZL) , ce qui est bien la formule obtenue avec le générateur de tension. La grandeur qui permet de passer de la valeur de la tension d'entrée Ve à la valeur du courant I généré s'appelle la transconductance. On voit qu'elle vaut ici A / Zs. Rappelons que A est une grandeur sans dimension. Donc la transconductance notée gm est homogène à l'inverse d'une résistance. Elle est exprimée le plus souvent en mA par volts.  Nous verrons que
cette grandeur est une
donnée fondamentale dans
l'amplification à tubes.
Méthode de
calcul d'une tension
de sortie fonction de
plusieurs entrées
indépendantes :
Le problème se pose ainsi : prenons le cas de deux tensions d'entrée donnant une tension de sortie fonction des deux entrées.  Comment
calculer Vs fonction
des deux tensions
d'entrée Ve1 et Ve2
INDEPENDANTES ?

Prenons
l'exemple le plus simple
du sommateur de tensions
sur une impédance
considérée comme
infinie. Nous
considérons les générateurs
de Thévenin Ve1
et Ve2 comme idéaux ,
avec une impédance de
sortie nulle.
 En appliquant la méthode citée plus haut nous commençons par mettre Ve2 à la masse pour calculer Vs1 = f(Ve1) : 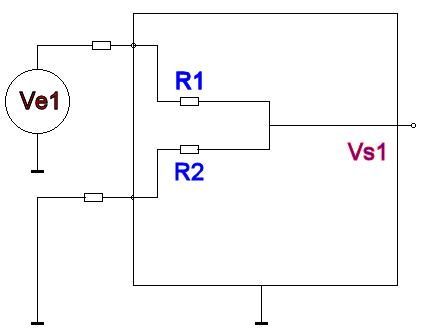 C'est
un simple
diviseur de
tensions. Il
apparaît :
 Faisons de
même avec Ve1 :
 Il
apparaît de même
:
 Il
en résulte que
:
 Cette méthode s'applique aux circuits simples comme aux plus complexes. Copyright ProjetG5 - Rédacteur jptrol mis à jour le 29 septembre 2018 |









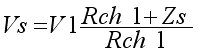 et
et





